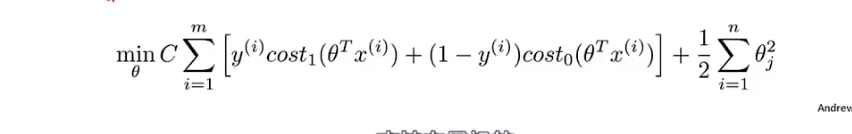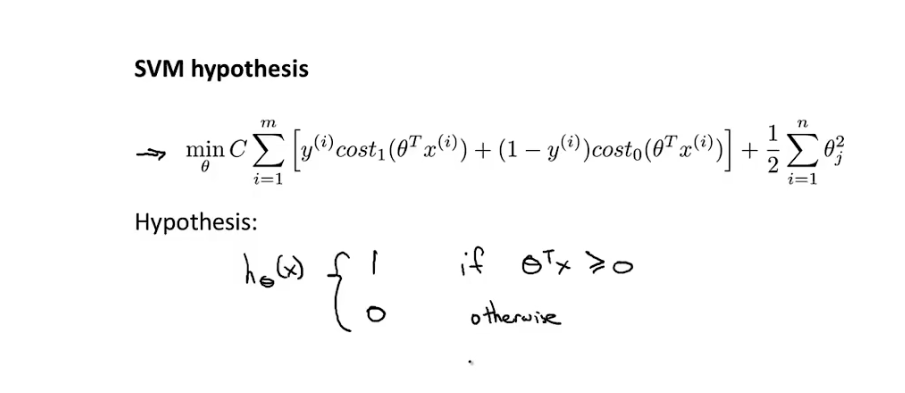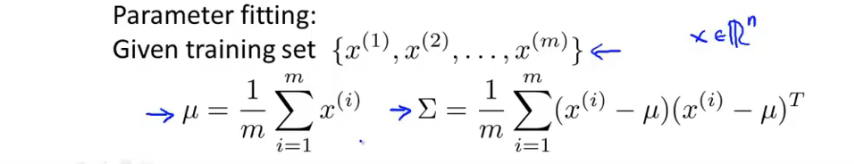Machine Learning and Deep Learning
监督机器学习
样本的值是具体已知的。
- 回归问题:根据数据集预测连续的数值
- 分类问题:根据数据集预测离散的数值
无监督机器学习
只有数据集没有任何标签(lable)与数值,自动找出数据的某种结构
2.线性模型
- 训练集:给出需要预测的数据集(x(i),y(i))
- 假设函数:h(x)=θ0+θ1x
- 代价(损失)函数:
3.梯度下降法
-
用于最小化损失函数J,求解目标函数系数。局部最低点
-
梯度:目标函数的等高线图 增长最快的方向,是一个向量。
-
-
初始化θ0,θ1,通常为0。
-
需要同步更新θ1,θ0
-
α:学习效率,梯度下降更新参数的速率
-
由于J需要整个训练集的样本,因此每次梯度下降需要遍历整个样本
-
二元线性回归函数各个系数的偏导:
-
线性函数梯度下降公式:
-
线性方程使用矩阵表示:
-
X * A = Y;
-
X: 行为不同维度的影响因子,每一行第一个通常为1,即常数项因子。列为数据组数。
-
A:系数矩阵:同一列为一组对应因子前的系数。
-
矩阵求逆:AA* = |A|I,A*为伴随矩阵:每个元素的代数余子式 构成的矩阵的转置。
-
代数余子式:M(i,j) = (-1)^(i + j) * |划掉所在行,所在列剩余矩阵。
-
-
4.多功能线性回归
4.1多特征
-
n:特征维度
-
-
用矩阵乘法来表示hypothesis formula:
4.2多元梯度下降
-
多元损失函数J(θ):
-
梯度下降中的偏导项:
4.3特征缩放
-
当多个特征的范围一致时:梯度下降速度块:
-
不一致时:速度慢。
-
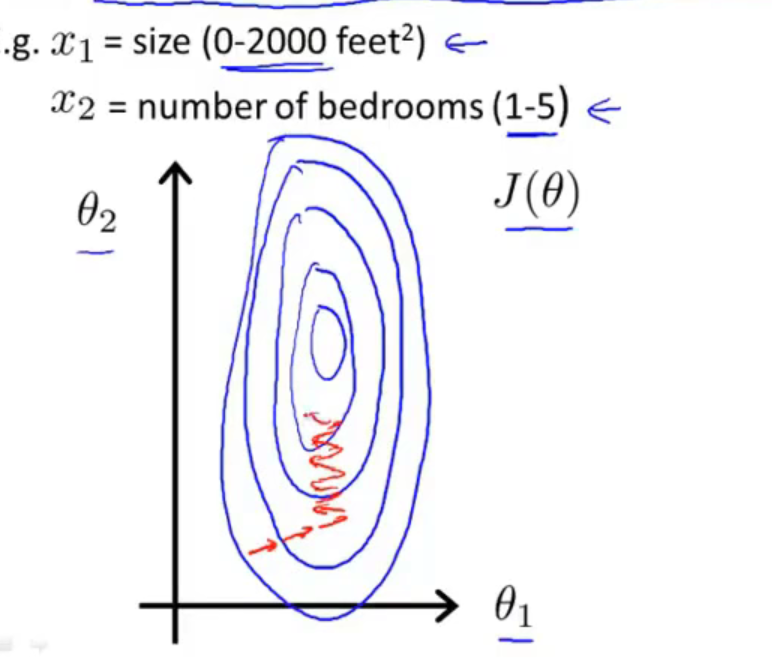
假设hypothesis有两个参数:θ1>>θ2 。损失函数的对应的等值(高)线:
-
-
根据梯度公式:
-
范围越大的哪个特质值,梯度中对应参数参数值越大。
-
-
-
通常特征缩放:将特征范围缩放在:-1<= x <= 1
-
常用方法:均值归一化:
-
4.4学习率:
- 学习率过大:反复横跳,不收敛。
- 小:梯度下降速度慢。
- 通常画出损失函数 J(θ) 与梯度下降递归次数的函数图像。应该是个单调递减图像。
4.5特征与多项式回归
- 多项式可以将高次项换元成一次项 变成线性回归。
4.6正规方程
-
给定一组样本数据 与 预期结果,用矩阵表示为:
-
正规方程:
-
证明过程:
-
正规方程与梯度下降:
- 梯度下降:
- 需要选择学习效率α,需要迭代
- n很大时仍然可以很好的运行
- 正规方程
- 不需要选择学习效率,也不需要迭代
- n很大时不能很好的运行,计算矩阵的逆开销很大O(N^3)
- 线性回归模型中,数据特征少时可以替代梯度下降
- 梯度下降:
-
-
正规方程矩阵不可逆时(奇异矩阵\退化矩阵):
- 可能是有两列(不同特征)是线性相关的,那么就删除一个特征。
- 可能是特征值过多,则删除一些特征值。
5.分类:逻辑回归算法
5.1 二分类问题
-
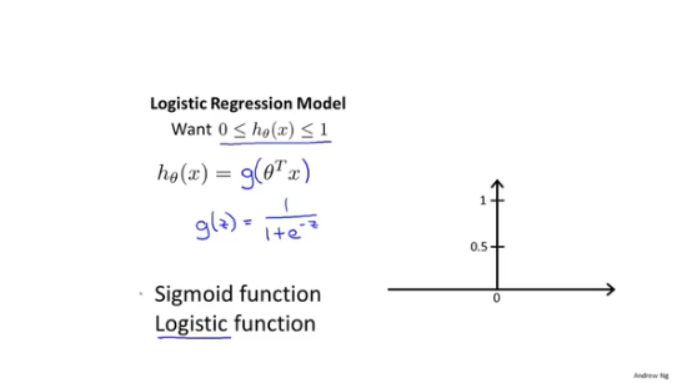
logical function/sigmod function:
- 输出:二分类:
- 概率
- P( Y = 0 | x;θ) = 1 - P (y = 1| x;θ)
- 输出:二分类:
-
决定边界
- θX
- θX >=0,out>0.5
- θX<0,out<0.5
- 决策边界不是由数据集决定,给定θ即确定一个决策边界,数据集不断地拟合决策边界。
-
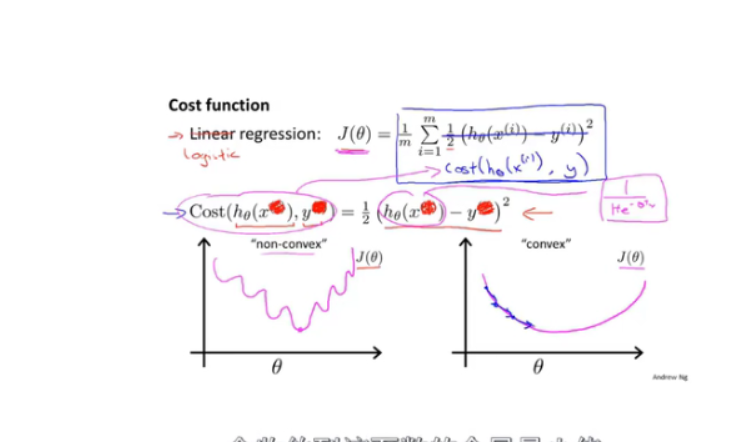
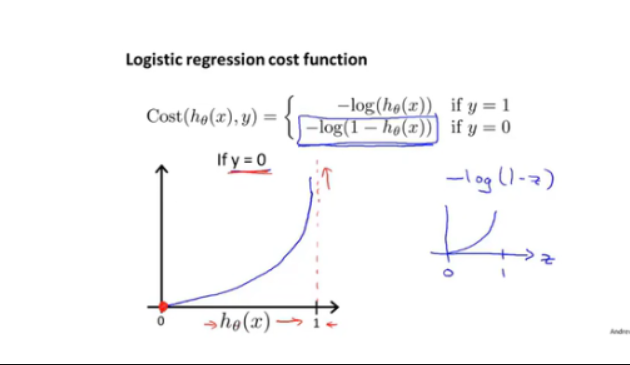
代价函数
-
由于sigmod为非线性函数,代价函数不是凸函数,梯度下降会找到局部最优解。
-
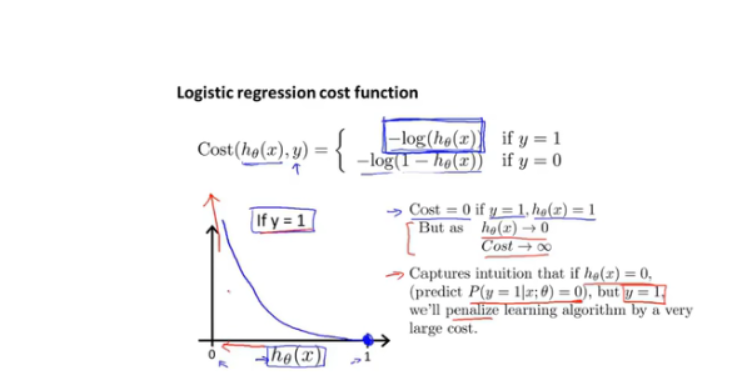
采用新cost_func
-
连续性cost_function:
-
极大似然估计法得出地cost_func
-
-
梯度下降算法:拟合θ
-
其他算法:
- Conjugate gradient
- BFGS
- L-BFGS
- 不需要手动选择学习效率
-
5.2 多分类问题
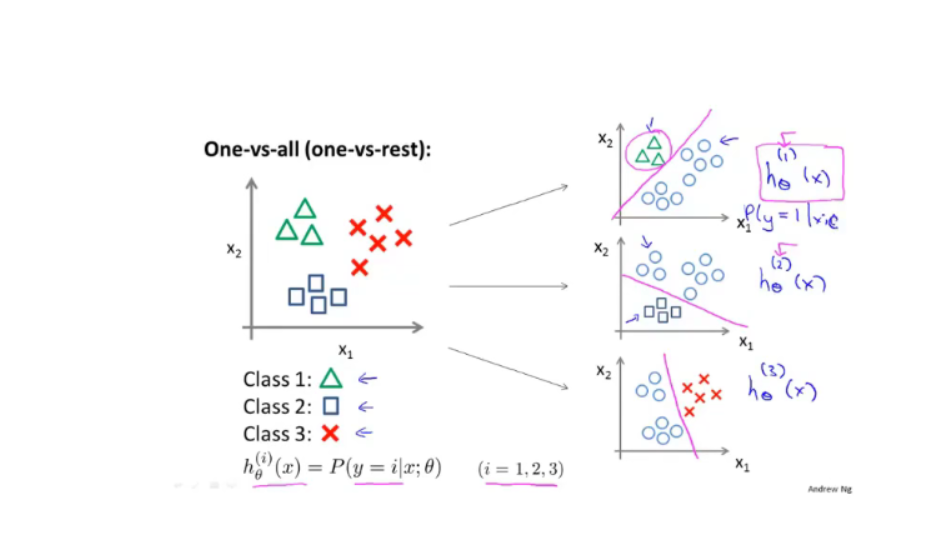
5.2.1一对多
-
使用多个二分类器函数:拟合出多个决定边界
-
预测:x特征值输入每个分类器,得到的最大值:
5.3 过拟合
5.3.1线性回归正则化
-
特征值过多,数据集过少
-
解决:
-
减少特征向量
-
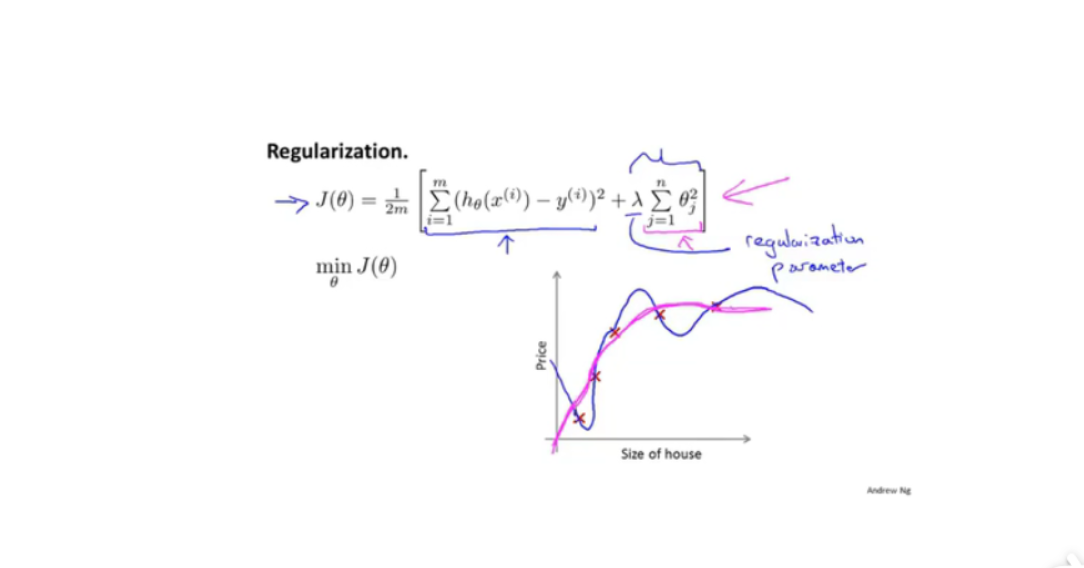
正则化 ( 减少规模/或者参数θ的大小)
-
正则化方程
- 前一半为优化参数目标损失函数,后一半为正则化参数参数平方之和,会使得每个θ都适当减小。
- 正则化参数太大,使得惩罚系数过大,θ1到θj都趋近于0,而退化成水平直线。
-
正则化后的梯度下降:
-
正规方程使用正则化:
- 同时解决了X^T*X 矩阵不可逆的情况。(m < n)
-
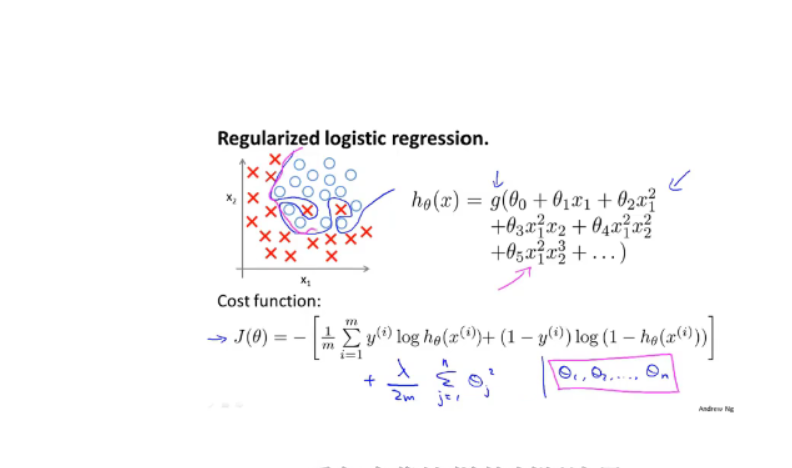
5.3.2 logical回归正则化
-
同理线性回归的损失函数:
-
梯度下降:
-
高级优化函数使用正则化:
-
自定义costFunction函数计算损失,和梯度:
-
-
6 神经网络
6.1 模型展示
-
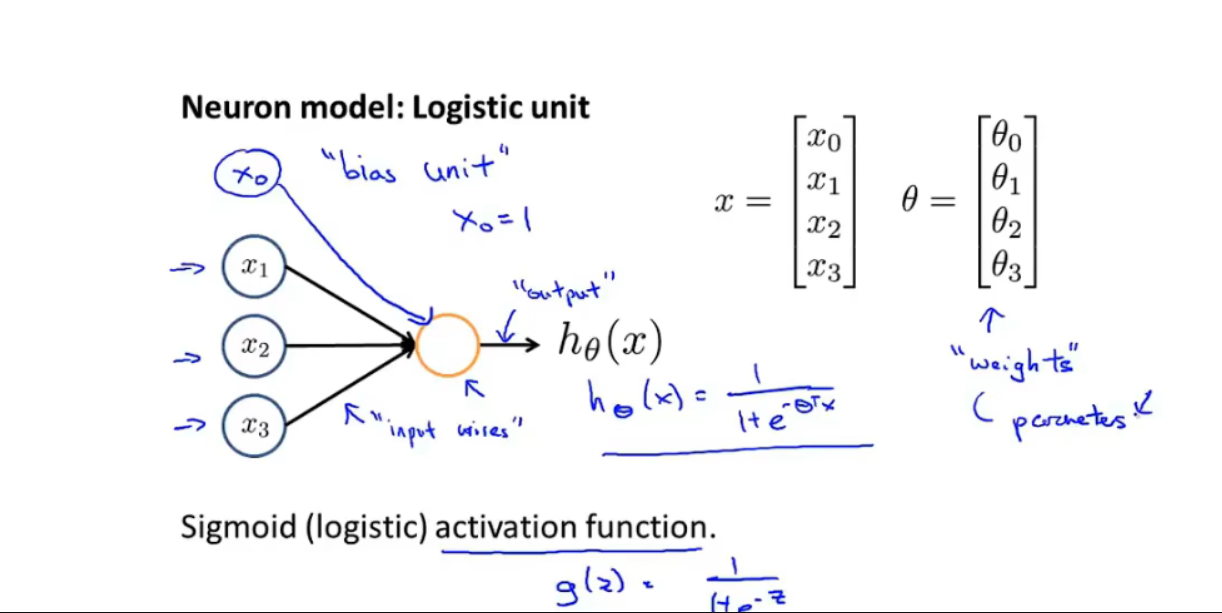
神经元
-
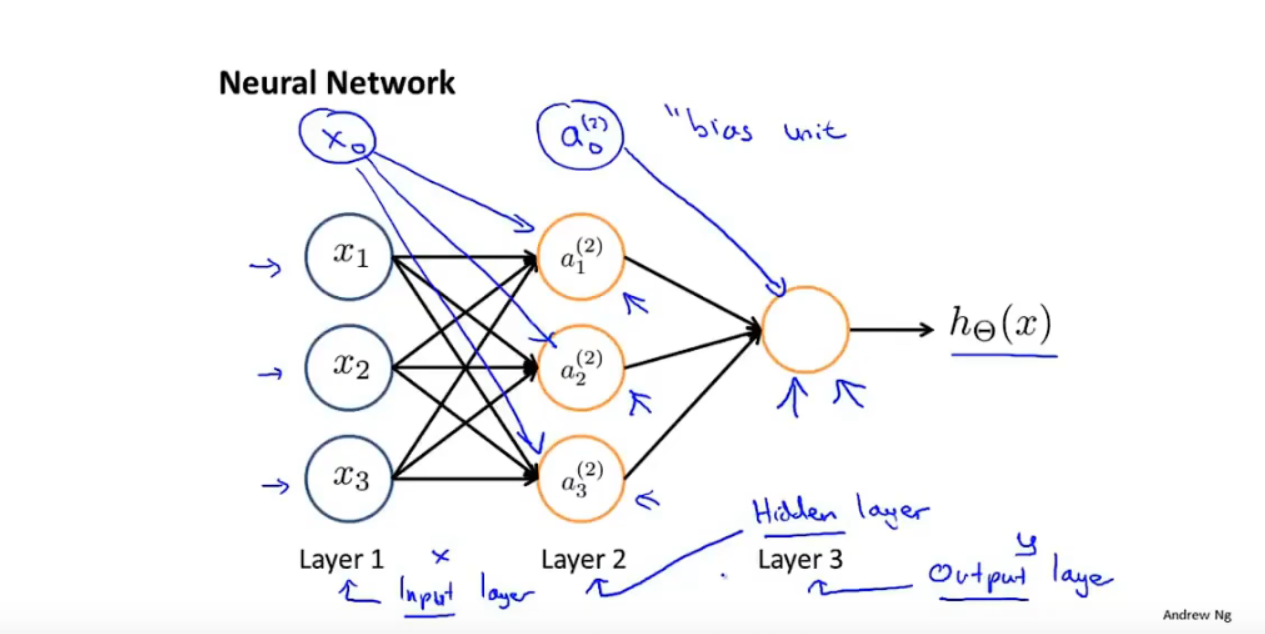
神经网络
- 输入层(Input layer):
- 神经元,激活层(activation function:sigmoiod function)
- 隐藏层(hidden layer)
- 输出层 (out layer)
- 权重
-
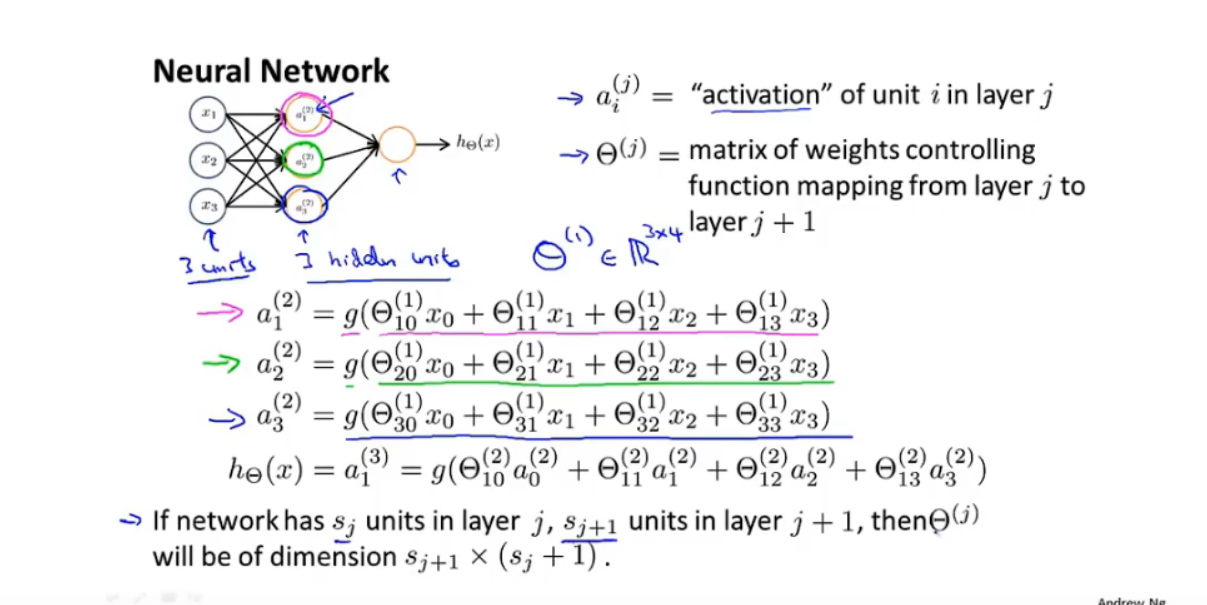
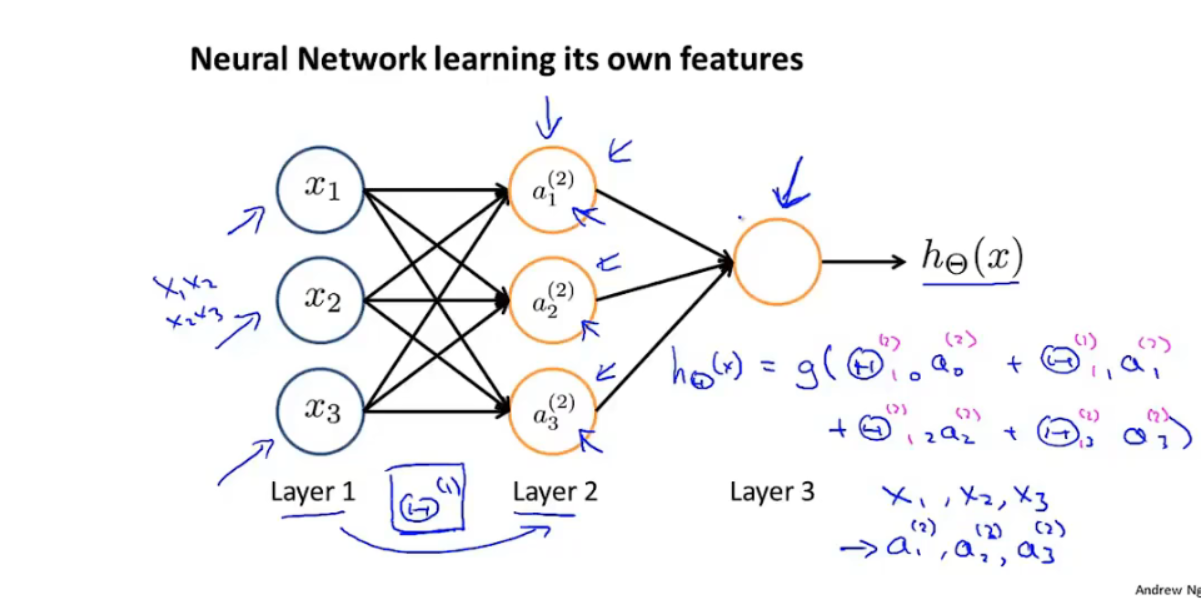
计算过程:
-
说明:
- θ矩阵:j层到j+1层的权重矩阵,用于计算下一层的输入,维度为:S(j+1) * (Sj + 1):
- Sj+1行θ
- 每一行Sj + 1个 权重参数
- θ矩阵:j层到j+1层的权重矩阵,用于计算下一层的输入,维度为:S(j+1) * (Sj + 1):
-
6.2 模型展示
-
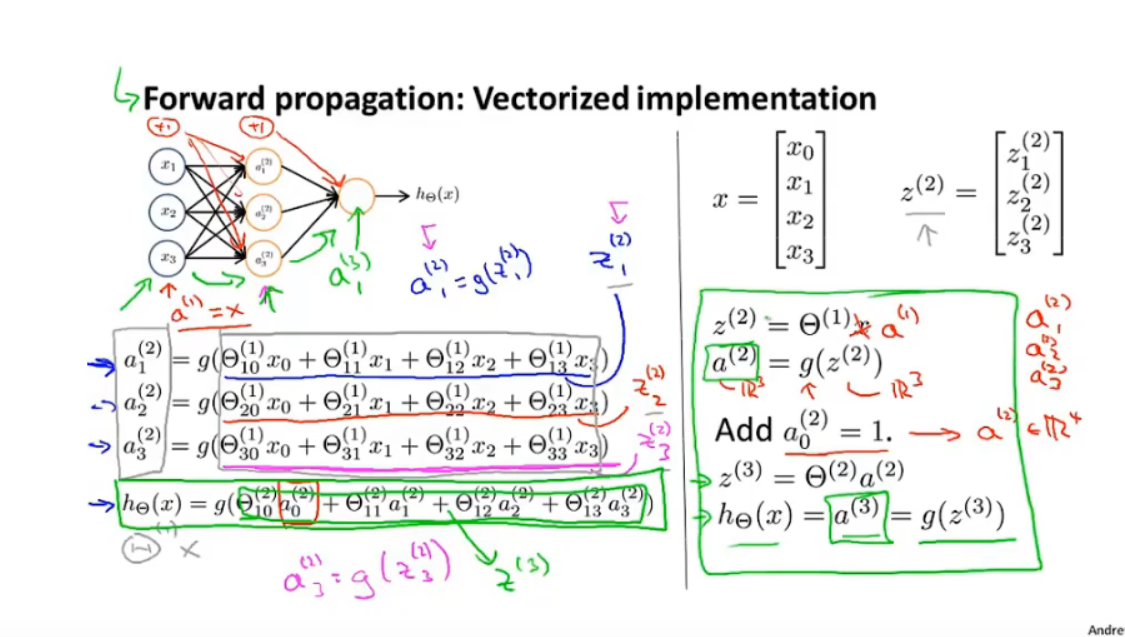
前向传播
-
使用隐藏层的输出作为 logistic regression 的输入特征:
-
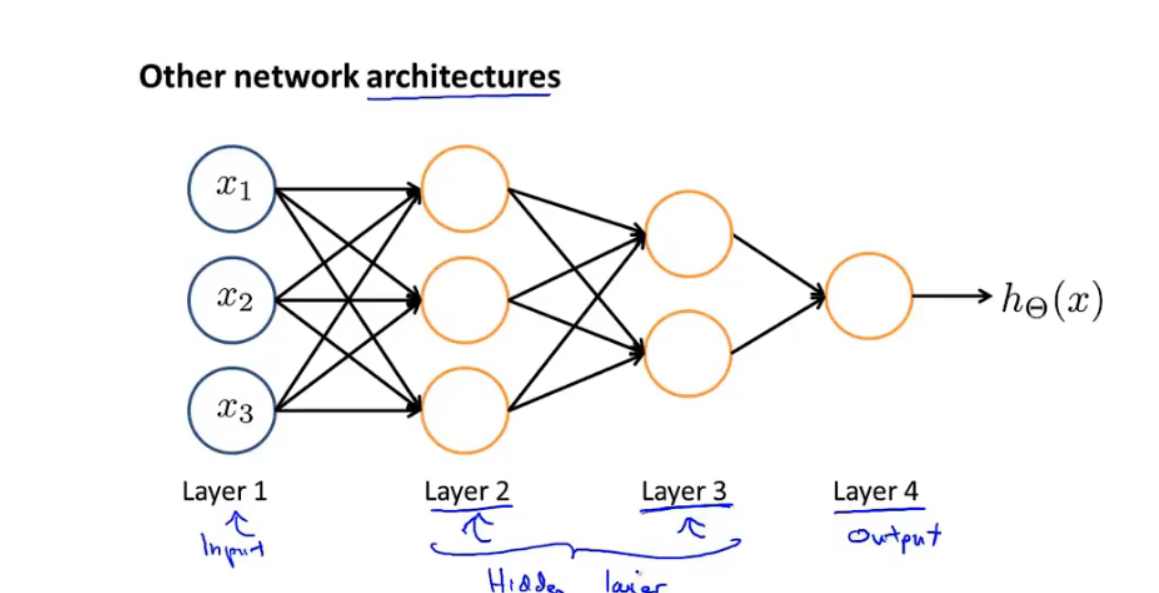
神经网络架构:神经元的连接方式
6.3例子与直觉解释
-
神经网络用于学习复杂的非线性假设模型
-
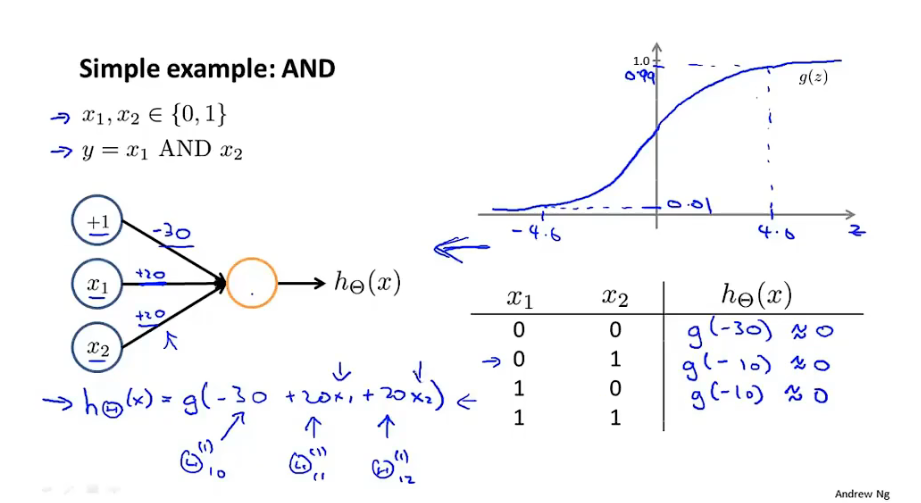
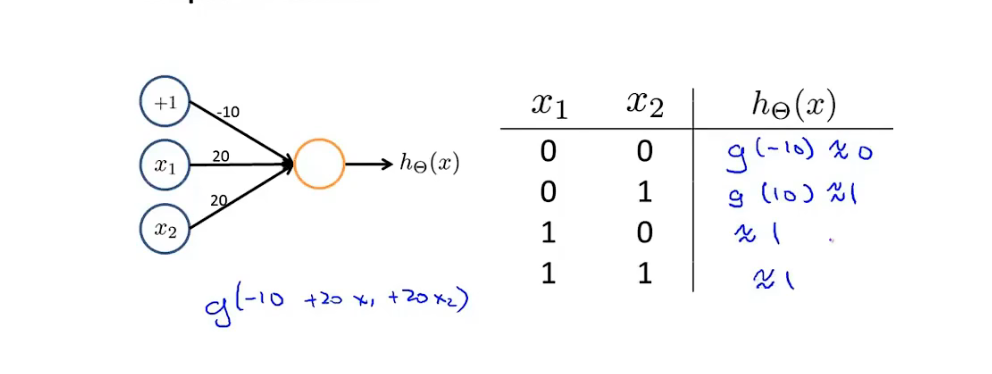
AND 逻辑函数拟合:
-
OR 逻辑拟合
-
NOT 逻辑拟合
-
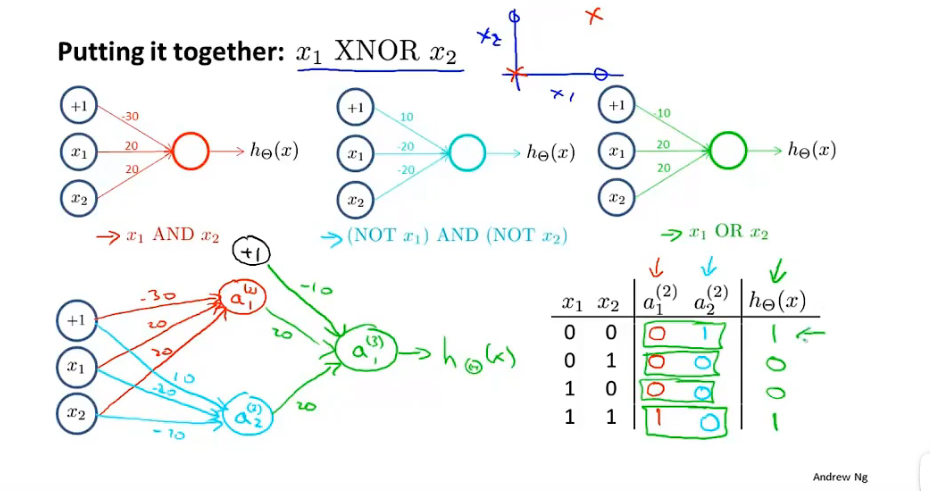
XNOR(同或)
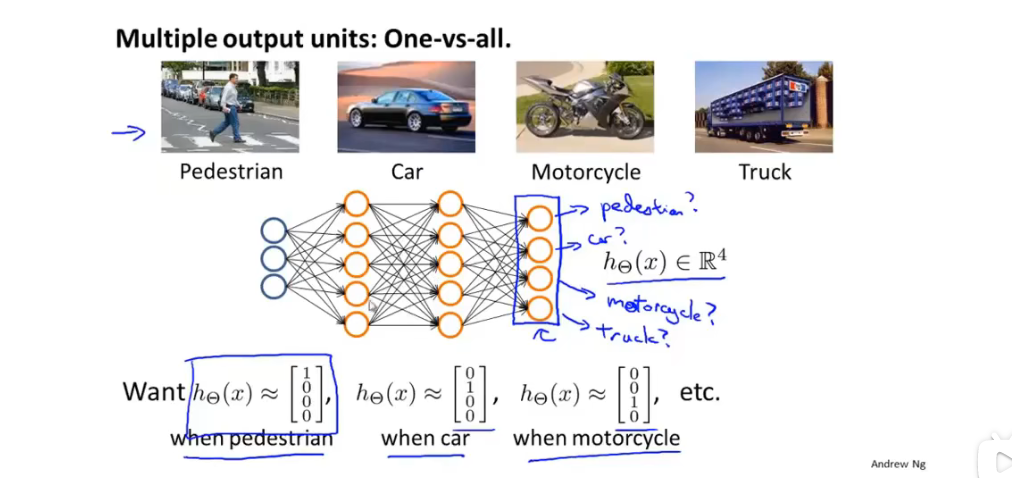
6.4多元分类
- 一对多:
7 神经网络原理
7.1 代价函数
-
神经网络代价函数
-
分类模型
-
-
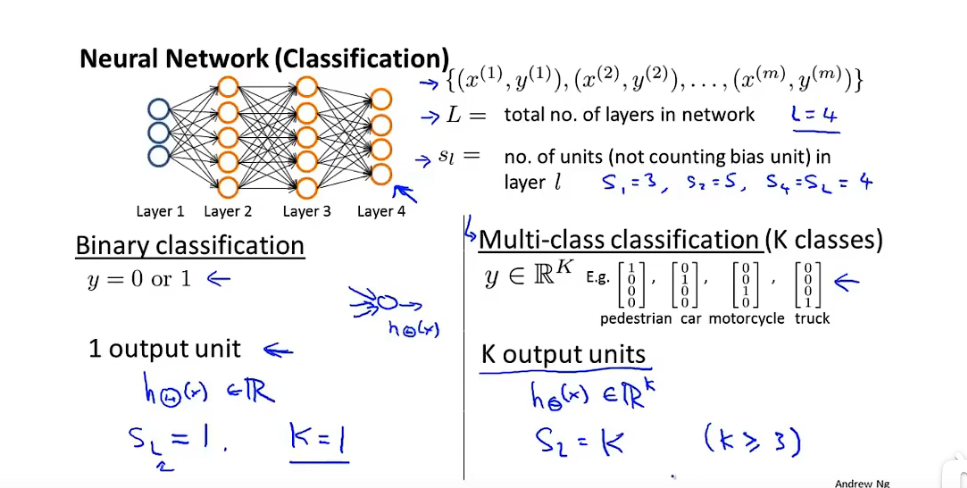
L :神经网络层数
-
S_l: l层神经元个数,不含偏置单元
-
-
损失函数
-
逻辑回归损失函数
-
神经网络损失函数:逻辑回归一般表达:
-
-
每一类的交叉损失函数 求和“1–K
-
正则参数:j:θ矩阵行数,i:θ矩阵列数,未算偏置参数
-
-
7.2 反向传播算法
-
损失函数
-
前向传播
-
反向传播:
-
误差 :定义:误差可根据反向传播获得
-
根据误差可求权重偏导:
-
”误差“计算:根据链式法则:详细解释: 吴恩达机器学习视频–神经网络反向传播算法公式推导_xuan_liu123的博客-CSDN博客_吴恩达反向传播
- 点乘:矩阵同位置元素相乘
-
多样本:上标i 与下标i不同意义:
-
-
向量化:
- Δ与Θ矩阵同行列,行:L+1层神经元个数;列:L层神经元个数
- 最终的梯度:
- j=0,对应的每层的偏置项,没有正则项
-
-
总结:
-
公式一:
-
公式二:
-
公式三:
-
-
根据这三个公式,可以完成反向多样本反向传播算法:计算出每个θ的偏导项
-
-
7.3 梯度检测
-
梯度的近似值计算 并与梯度进行比较
-
-
-
训练时关闭 梯度检测 方法:降低算法效率。
-
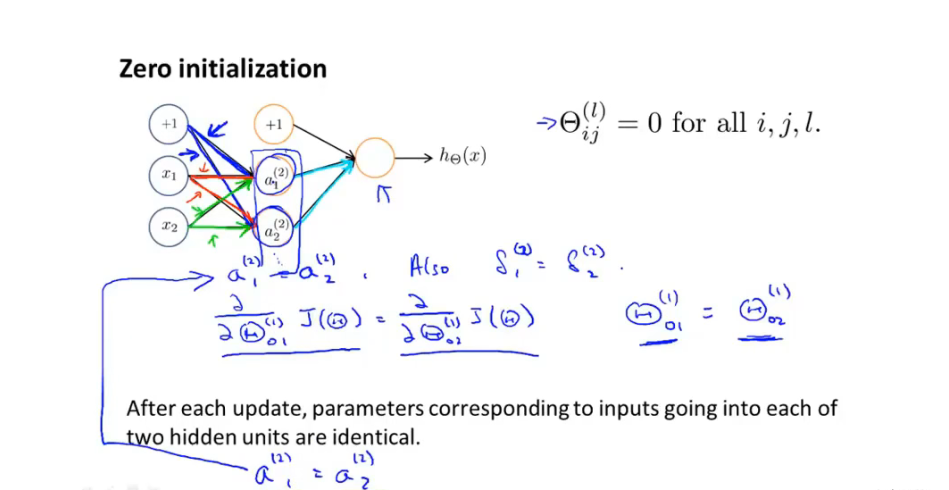
7.4 随机初始化
-
初始化全为0:
-
-
所有的输入输出值都为相同的值和函数
-
7.5 总结
-
神经网络架构:神经元之间的连接方式。
- 输入:特征值的维度
- 输出:分类的个数
- 合理的默认架构:一个隐藏层,或者多个隐藏层的神经元个数相等
-
训练神经网络步骤:
-
-
-
搭建神经网络并随机初始化参数值
-
实现前向传播计算每层输入与输出值
-
实现损失函数
-
实现反向传播计算每个参数偏导项
-
使用梯度检测 检测梯度近似值是否符合要求,训练前关闭梯度检测
-
使用梯度下降或者其他优化算法 优化损失函数。
-
8 机器学习算法诊断
8.1 评估假设
- 防止过拟合:
- 正则化
- 减少多余特征
- 划分数据集,7:3 训练集+测试集
- 使用测试数据集 计算测试误差
8.2 模型/特征选择,训练,验证,测试数据集
- 增强模型泛化能力
- 将数据集划分为 训练集 验证集 测试集6 : 2 : 2
- 训练集误差, 验证集误差,测试集误差
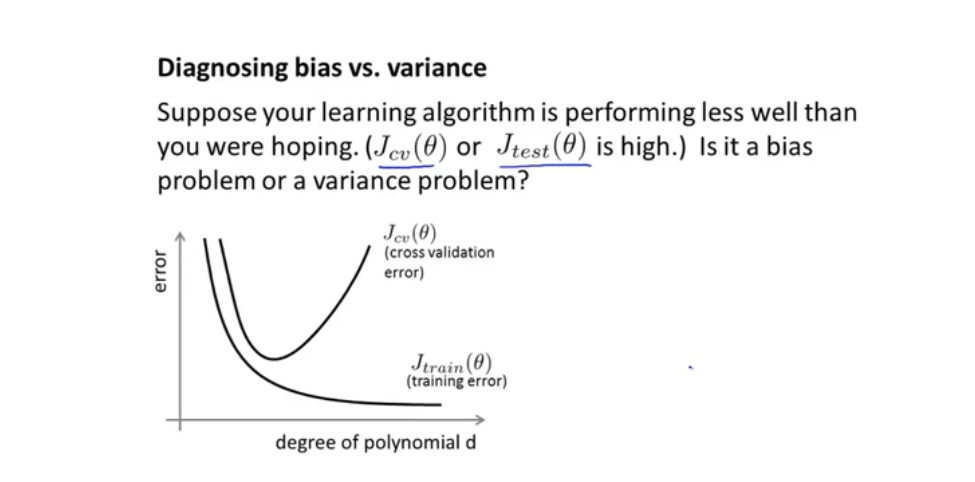
8.3 诊断偏差与方差
-
验证集误差与训练集误差 图:
-
-
高偏差问题:左边,欠拟合,训练集验证集误差都很大
-
高方差问题:右边,过拟合,训练姐误差小,验证集误差大
-
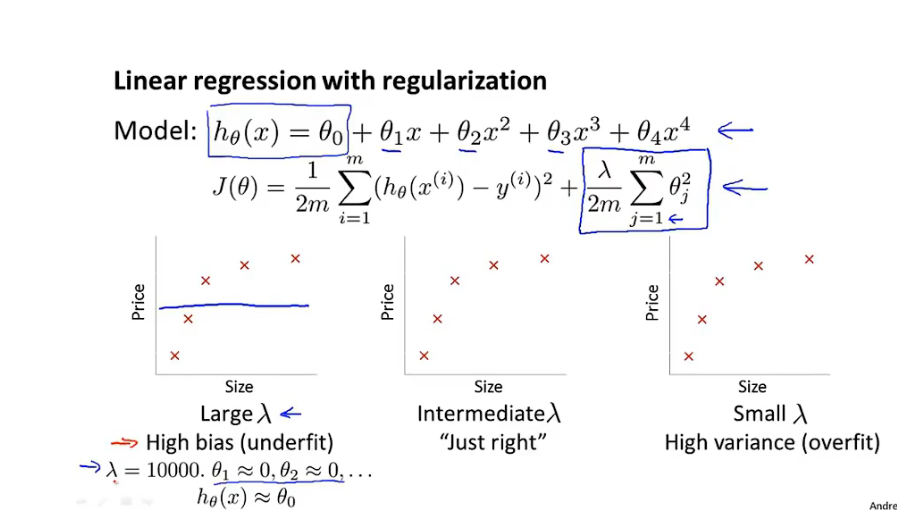
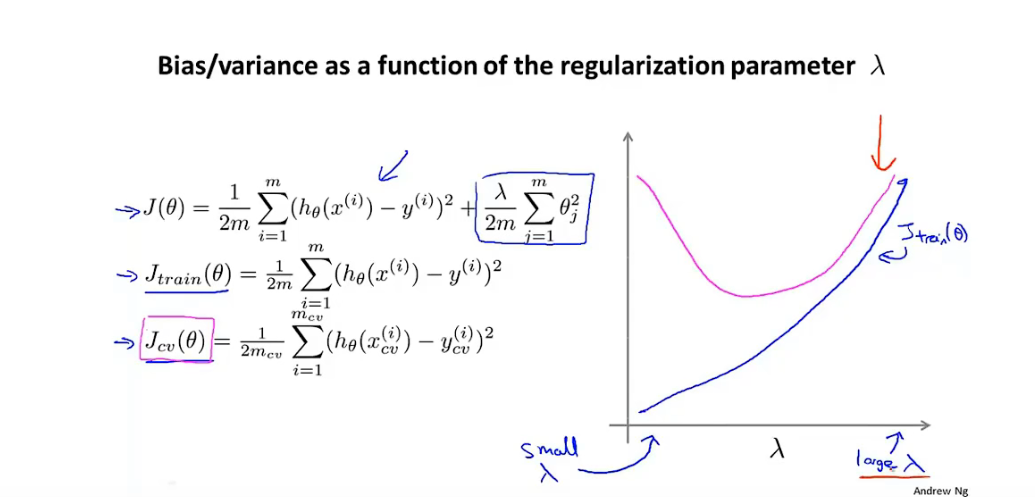
8.4 正则化与偏差,方差
-
正则化参数过大:
- 欠拟合,训练数据集和验证集误差都大,偏差问题
-
正则化参数刚好
-
正则化参数过小
- 过拟合,训练集误差小验证集误差大,方差问题。
-
-
如何选择正则化参数
-
正则化参数图
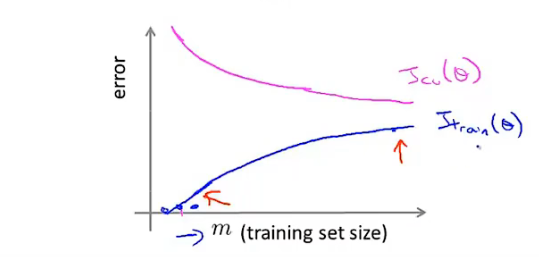
8.5 学习曲线
-
学习曲线:检验算法是否正确,是否存在偏差,方差问题
- y轴:误差
- x轴:数据集大小
-
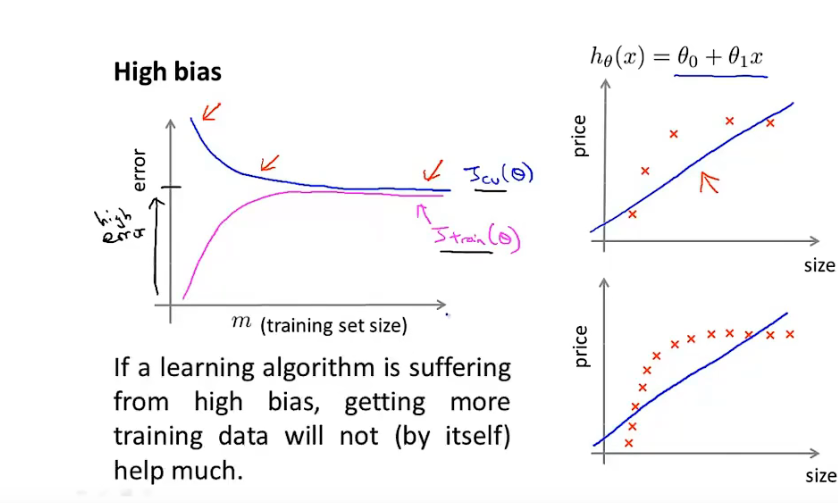
高偏差:high bias
-
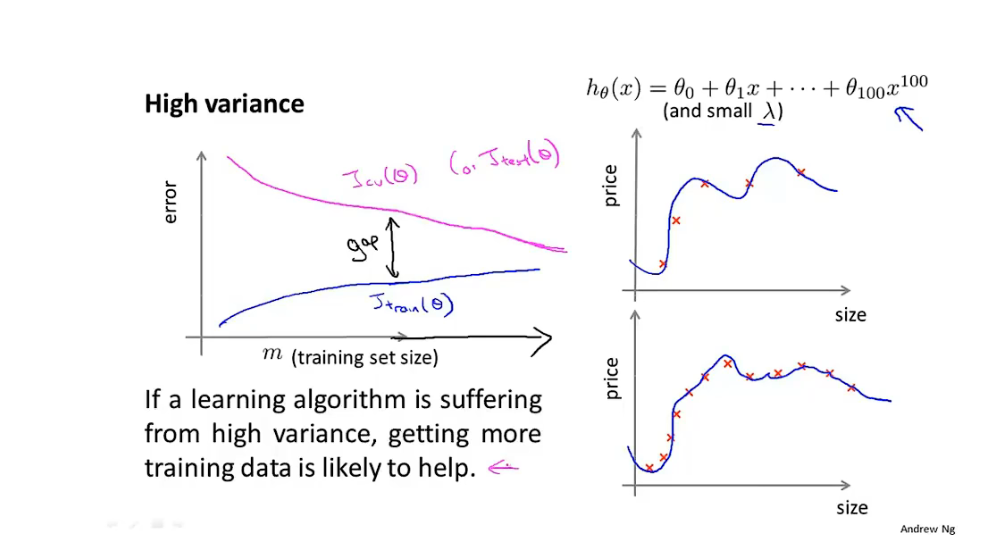
高方差:high variance
-
选择优化方法:
-
过拟合/高方差问题:获取更多数据集,减少特征数量,正则化,提高正则化参数
-
欠拟合/高偏差问题:获取更多特征,添加其他多项式特征,减小正则化参数
-
9 机器学习系统设计思想
9.1不对称分类误差评估
- 偏斜类问题:数据集中其中一类的数据过多或过少
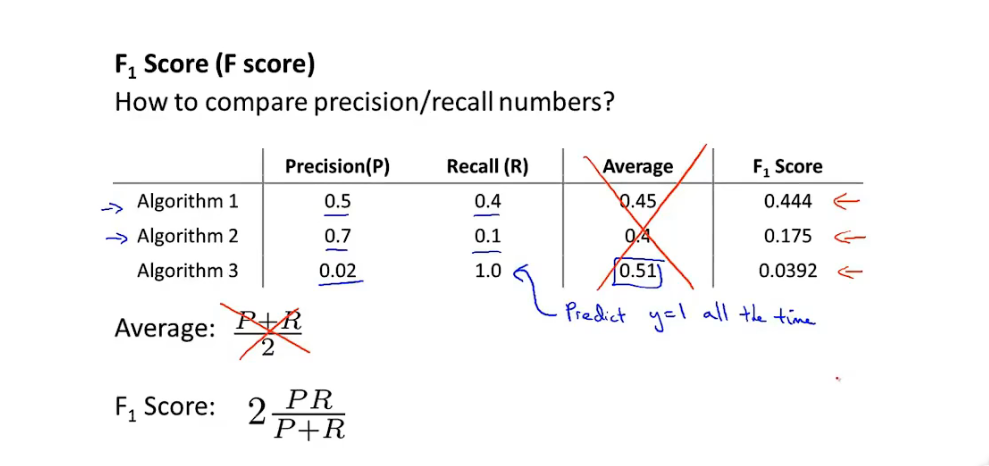
- 偏斜类问题 需要一种新的评估参数:查准率/召回率(Precision/Recall):
-
- Precision查准率:某一类准确预测数/预测为该类的总数
- Recall 召回率:某一类准确预测数/该类的总数
- F score:
10 支持向量机 SVM
10.1优化目标
-
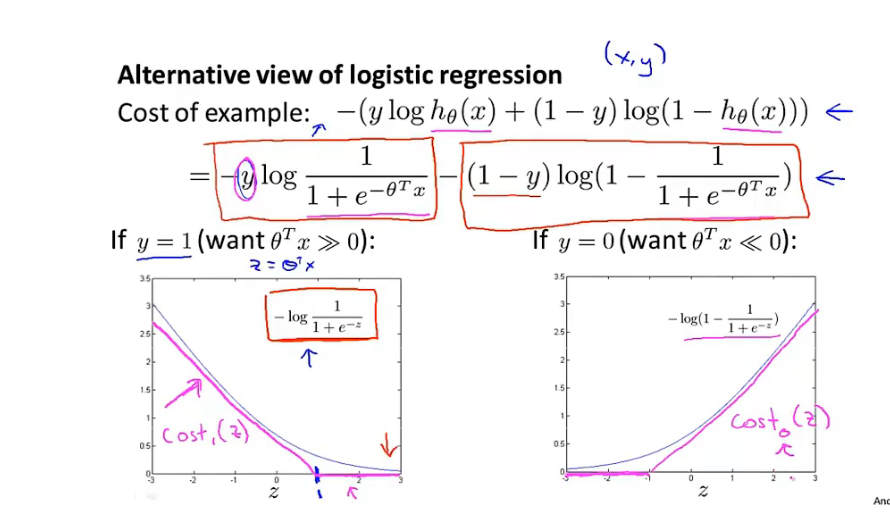
损失函数:对逻辑回归损失函数做一点小修改
-
-
- 参数C 与正则化参数 λ相同的作用
-
SVM 不输出概率 而是直接进行分类输出
-
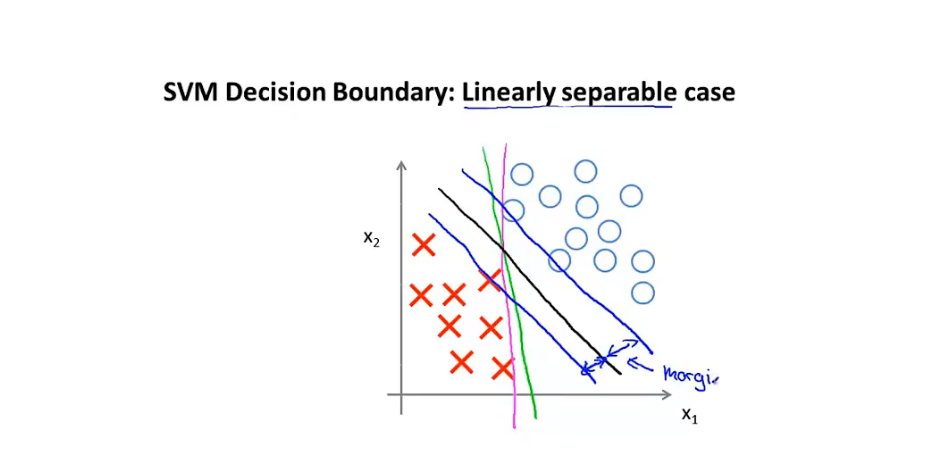
10.2 大间距分类器
-
- 对比于逻辑回归,当y=1时,z>=1时,才能预测为1
- y=0时,z<=-1时才能预测为0
-
SVM 决策边界:
- C十分大的情况下 拟合出来的决策边界:存在一个SVM间距
-
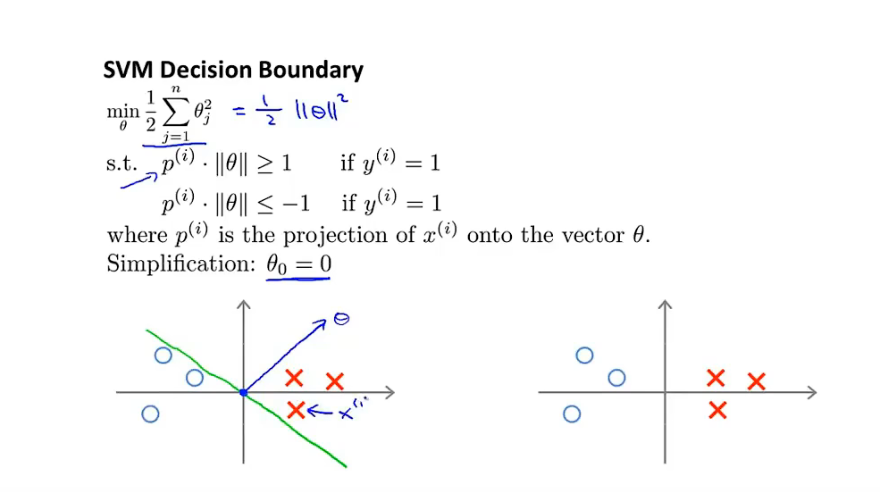
数学原理
-
假设只有两个特征,θ0=0
-
-
θX=0为决策边界,因此θ向量与决策边界正交
-
此时X向量向θ向量投影会非常的小,满徐限制条件则θ向量的模 需要十分大,此时J损失函数误差大,因此此 决策边界不行
-
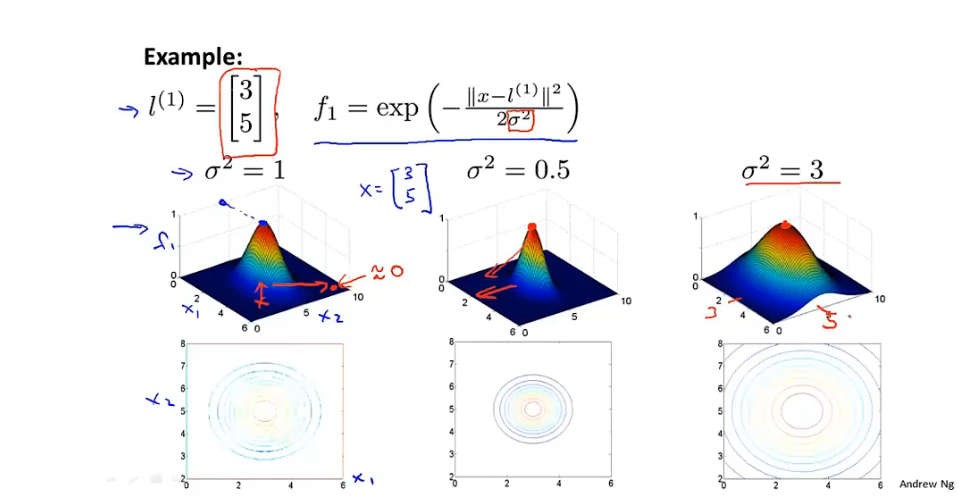
10.3 核函数
-
相似度函数:高斯核函数:
-
-
-
核函数图
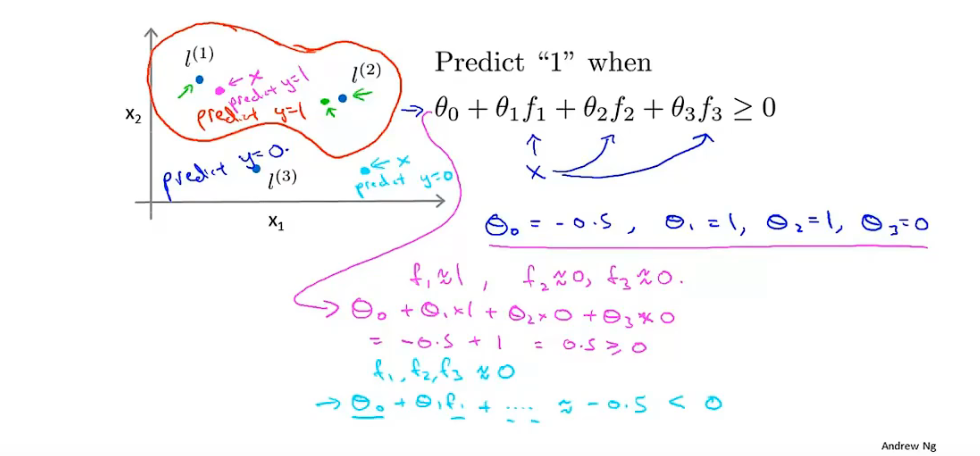
-
核函数与决策边界:
-
-
标记点 landmark:
-
直接选取样本点为landmark:
-
将样本点特征值映射到新的特征空间:维度发生了变化
-
-
-
SVM参数C
- C大:低偏差,高方差(过拟合)
- C小;高偏差,低方差(欠拟合)
-
SVM参数 ð
- 大:高偏差,低方差(欠拟合)
- 小:低偏差,高方差(过拟合)
使用SVM
-
指定参数C
-
指定核函数
- 线性核函数:初始特征维度n大,数据集m小,使用非线性容易过拟合
- 高斯核函数:初始特征维度n小,数据集m大
- 提供核函数计算方式:
-
核函数需满足 莫塞尔定理
- 多项式核函数
- 字符串核函数,卡方核函数,直方核函数
- 多项式核函数
-
逻辑回归与SVM
- 特征维度 n >> m
- 线性回归,线性核函数SVM
- 特征维度 n小,m适中
- 高斯SVM
- 特征维度n小,m大
- 创建更多特征,使用逻辑回归 并 使用线性核函数SVM
- 特征维度 n >> m
11 无监督学习
- 数据集没有标签
- 通过算法找到数据集中的结构:聚类算法
11.1 K-Means 聚类算法
-
选取聚类中心 (cluster center)
-
首先进行簇分类:根据距离聚类中心的距离对样本进行分类
-
然后进移动聚类中心:计算同一类样本的均值并移动聚类中心到均值
-
重复进行迭代
-
K-Means 算法输入
-
-
聚类数目:K
-
无标签样本
-
-
K-Means 算法步骤
11.2 优化目标
-
优化目标:失真代价函数
-
-
使损失函数最小:
- 找到每个样本所属的聚类c参数
- 找到每个聚类的聚类中心
-
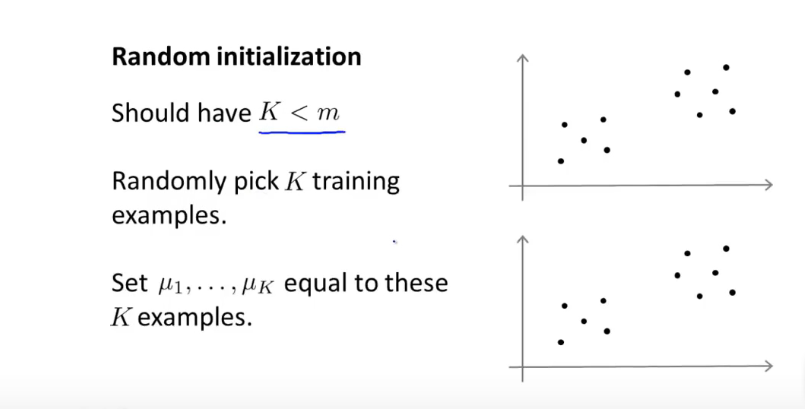
11.3随机初始化
-
随机初始化
-
-
聚类数小于样本数
-
随机K个训练样本作为 初始化聚类中心
-
-
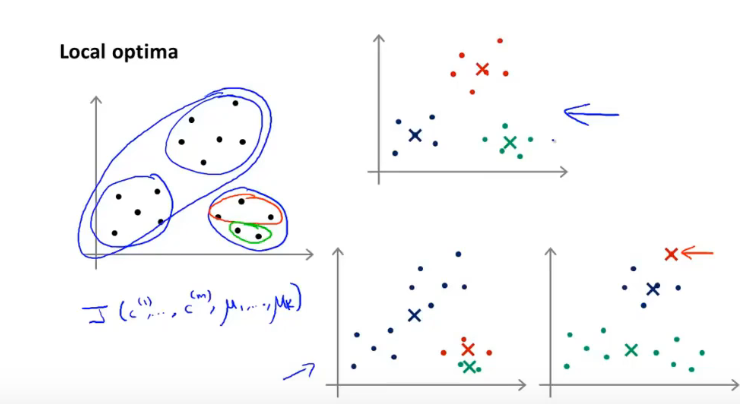
局部最优化
-
防止局部最优解,运行多次随机初始化并寻找最小损失函数解
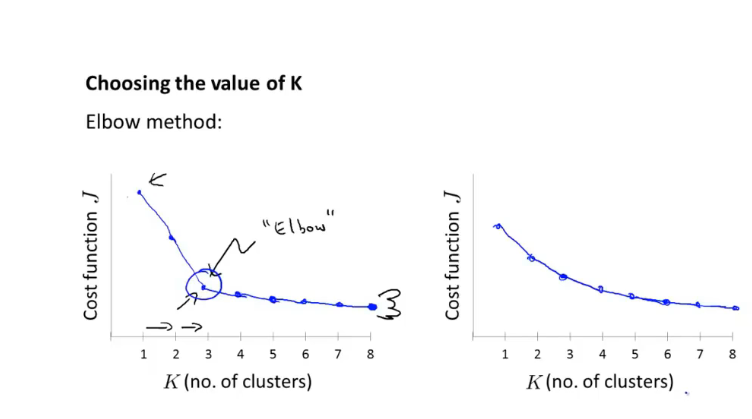
11.4 选取聚类数量
-
肘部法则
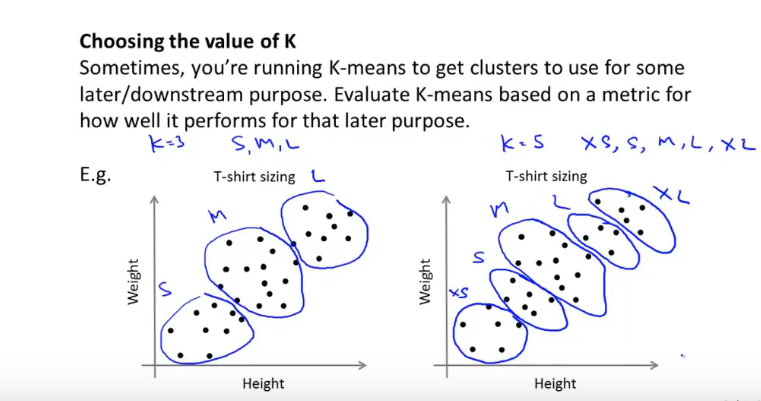
-
根据下游目的选择K的数量
12 降维
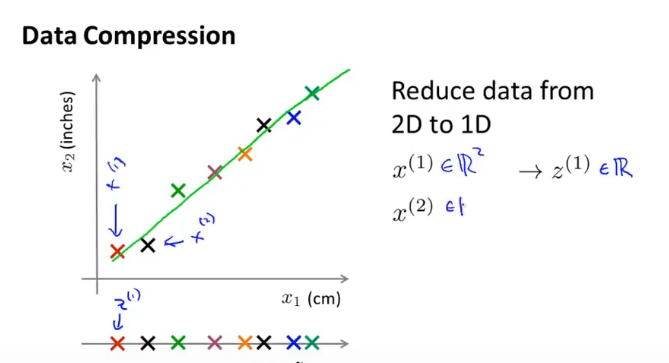
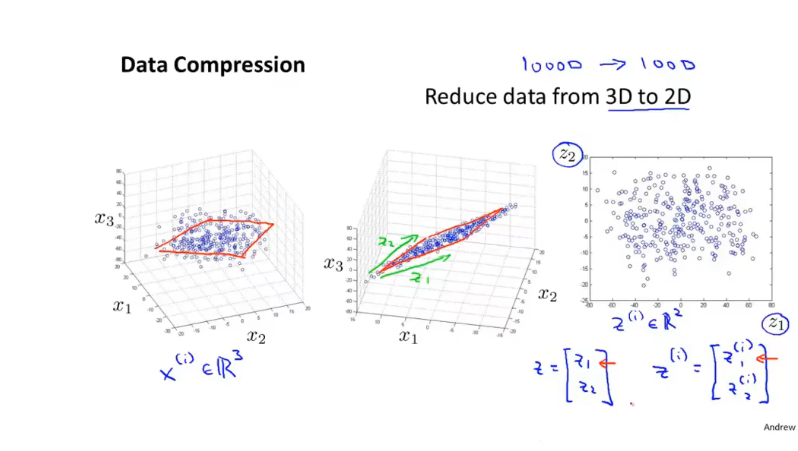
12.1 数据压缩
-
2D-1D:
-
3D - 2D
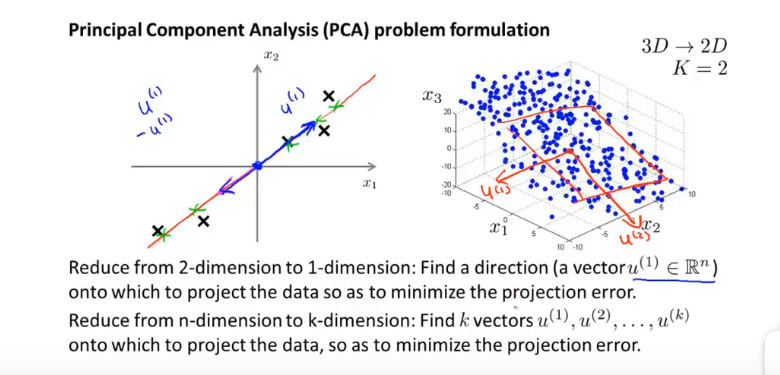
12.2 主成分析问题规划 PCA
-
将高维特征 映射到低维 空间
-
-
寻找K个向量组成的子空间,将n维向量映射到该子空间
-
-
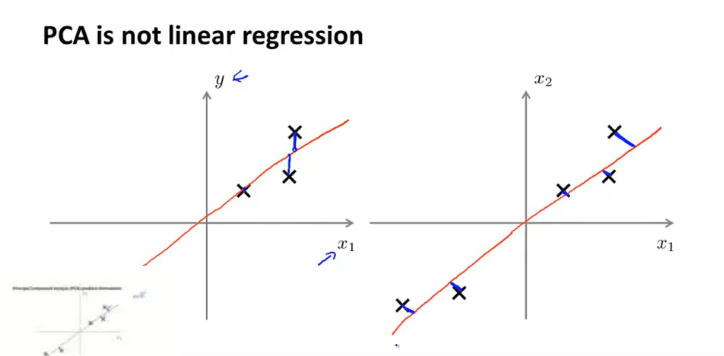
线性回归与 PCA:误差函数不一样
-
PCA算法过程
-
-
首先进行特征值的均值归一化/特征缩放
-
然后计算协方差矩阵,并运用奇异值分解计算协方差矩阵获得 前k个向量组成的低维子空间
-
最后计算 映射到低维的向量
-
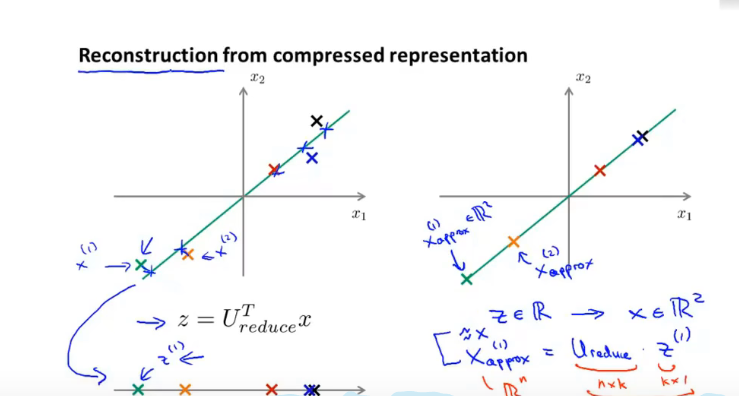
12.3 压缩重现
12.4如何选择K
- 确保该不等式小于等于一个小值:也称作保留了99%方差
- 如何查看该值是否满足要求,在svd函数中返回的矩阵即可求解,不需要反复计算该值:
12.5 PCA使用建议
-
应用:
- 数据降维加快算法效率
- 数据可视化
-
PCA不用于 防止过拟合
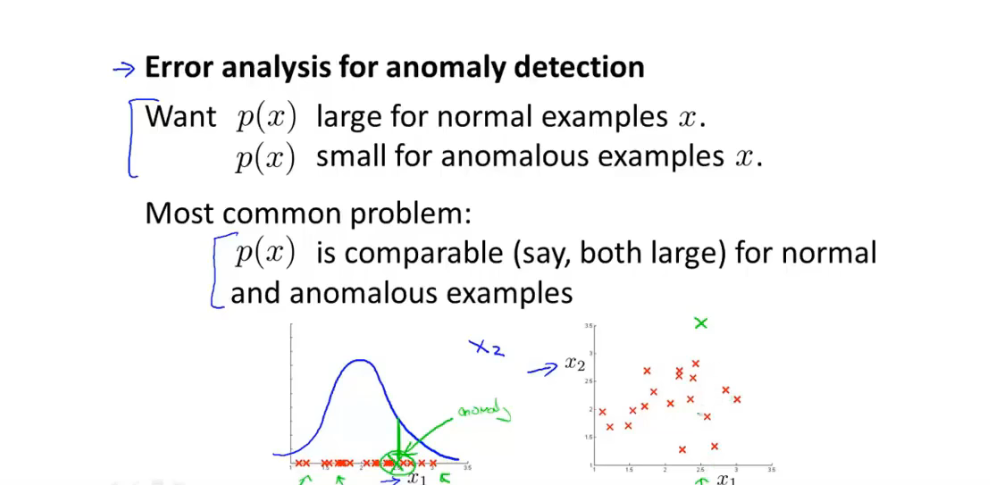
13 异常检测
13.1 问题动机
-
主要用于非监督学习
-
例子
-
-
- 用户欺骗行为检测
- 工业产品制造检测
- 数据中心集群检测
-
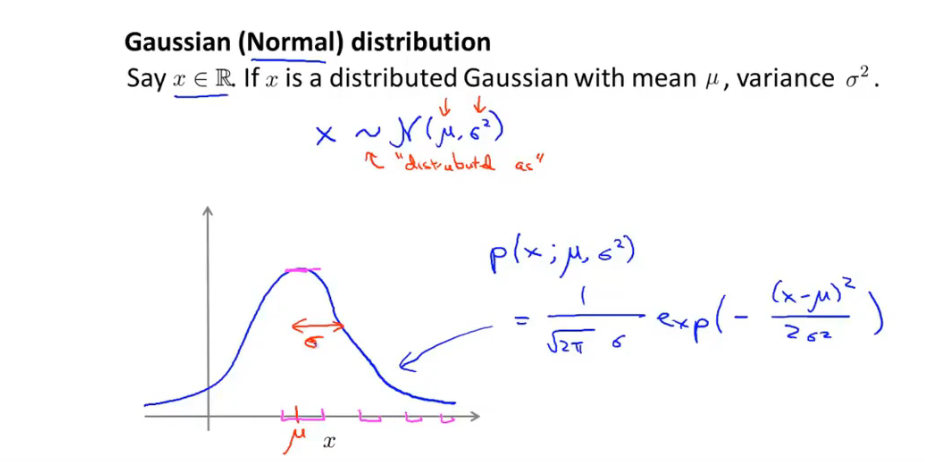
13.2 高斯分布(正态分布)
-
高斯分布:
-
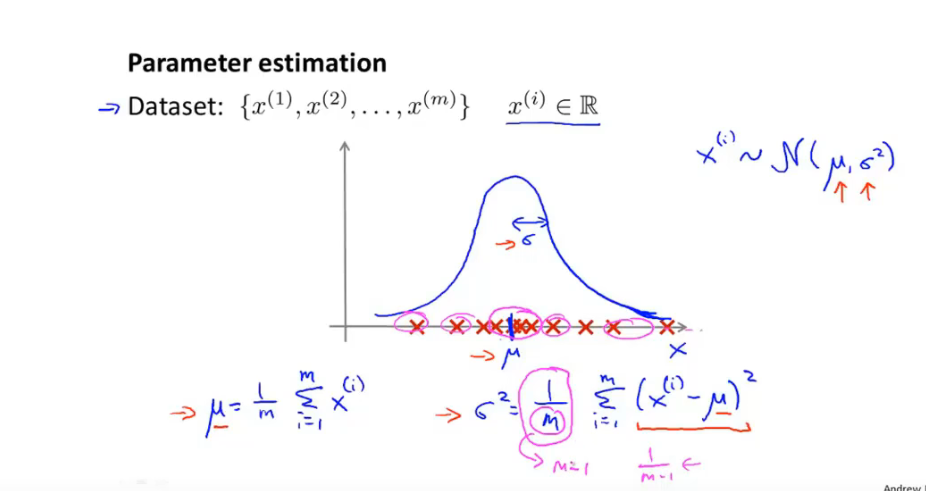
参数估计问题:给定数据集,拟合出数据集的概率分布参数
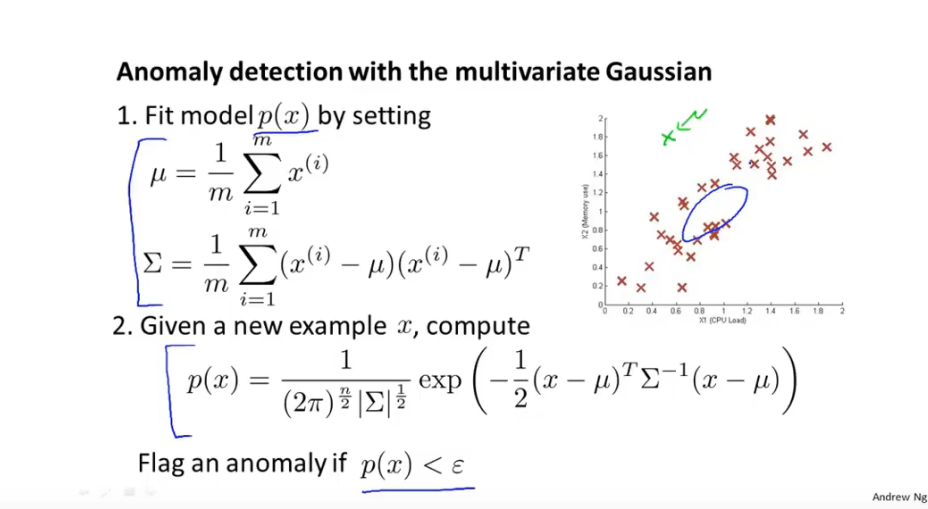
13.3 异常检测算法
-
(各个特征独立同分布/不独立也可以),假设概率模型P(x) 为:
-
算法步骤
-
-
选择特征值
-
计算拟合每个特征的 正态分布 参数并计算总的概率密度函数
-
带入新的数据参数 计算概率值
-
13.4 评估 异常检测算法
-
划分数据集
-
-
训练集:无标签
-
CV 交叉验证集:带标签
-
测试集:带标签
-
-
评估步骤
- 计算拟合模型P(x)
- 在 CV集 和test集 上计算 概率值并检验是否异常
- 计算画出评估矩阵,计算查准率和召回率 并计算 F-score
13.5 异常检测与监督学习
- 异常检测:正样本/负样本 很少
- 监督学习:正样本与负样本 都很多
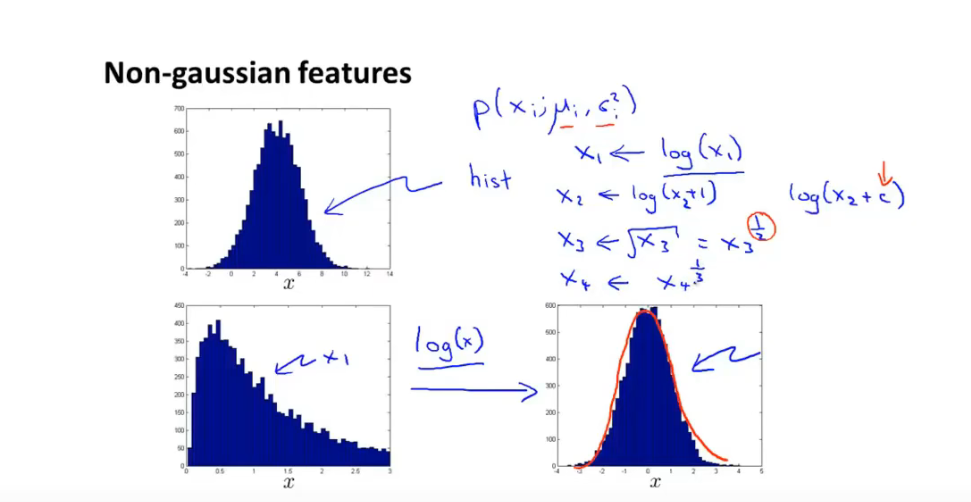
13.6 如何 选择 异常检测 特征
-
画出数据集中不同特征的直方图
-
误差分析:
-
-
从CV数据集中检查 被误分类的数据,并检查其中的特征,是否包含标志性特征
-
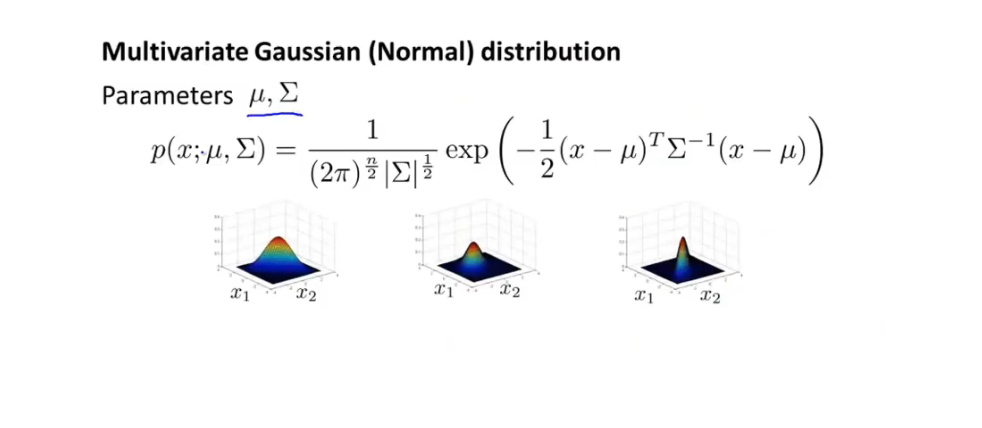
13.7 多变量高斯分布
-
多变量高斯分布 函数
-
-
通过数据集拟合 多元高斯函数 参数:
-
多元高斯分布函数 异常检测算法步骤
-
普通高斯函数模型与多元高斯函数模型
- 普通高斯函数时一种特殊情况:多元高斯模型 协方差矩阵非对角线值为0
- 多元高斯模型可以自动捕获特征之间的关系,普通高斯分布模型需要设置一个新的特征捕获特征间的关联,普通高斯模型计算性能更快
14 推荐算法
14.1 基于内容的推荐算法
-
例子:根据已有用户对不同 电影的评价,拟合出不同用户的 的参数,从而预测用户未看过的电影评价
-
-
假设每个电影有两个特征:浪漫程度和 动作指数
-
参数意义:
-
优化函数:
-
-
对每个用户j:有一个参数向量θ_j,总的优化目标函数将每个 用户的损失函数相加 并加上正则项
-
-
计算梯度
-
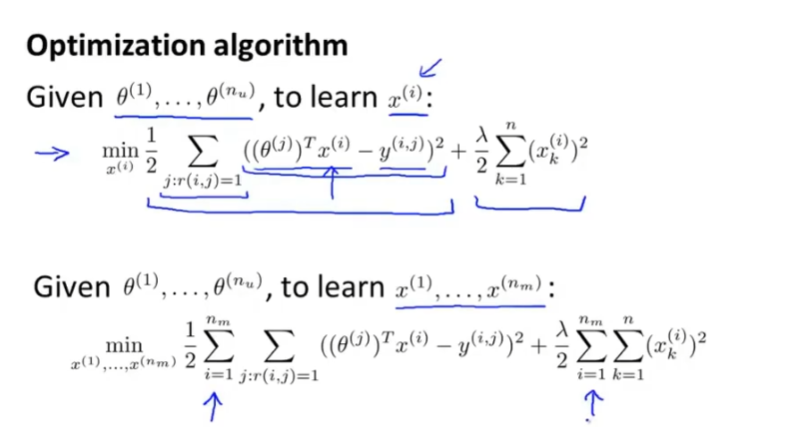
14.2 协同过滤
-
先提供参数 θ_j, 拟合出每个电影的特征值 x_i
-
优化目标:
-
-
对于每个电影的特征值 x_i,计算在已知θ_j 下的误差值并求和,再优化
-
-
协同过滤
-
-
随机初始化θ_j, 拟合出 特征值 x_i,再拟合出 θ_j ,直到收敛
-
-
将两个优化目标 函数结合在一起:
-
协同过滤步骤
-
-
随机初始化特征值 向量与 参数向量
-
优化算法 优化协同损失函数
-
对 用户未作评价的电影 根据拟合的 参数θ和电影的特征值进行预测
-
14.3 协同过滤向量化
-
低秩矩阵分解:
-
相似推荐:
- 根据学习到的特征向量,判断两个电影的相似程度:
- 根据学习到的特征向量,判断两个电影的相似程度:
14.4 均值归一化
- 将数据集均值归一化后进行训练:
15 大数据机器学习处理
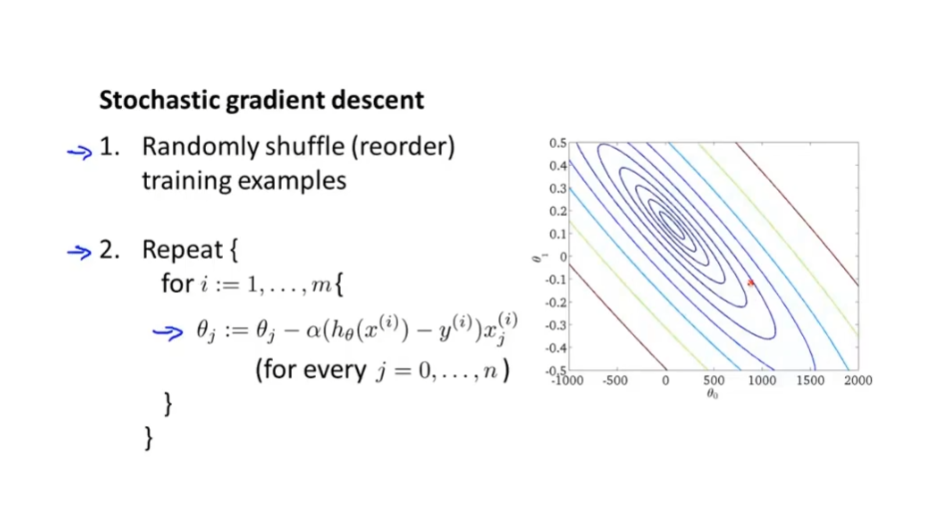
15.1 随机梯度下降
-
思想:在对数据集进行遍历一次的同时开始 对参数进行拟合优化,而不是需要进行多次遍历数据求和进行梯度下降。
-
步骤
-
-
随机打乱数据
-
对每个样本数据集 进行单个梯度下降,进行参数拟合
-
15.2 Mini-Batch 梯度下降
-
思想:介于batch 梯度下降与随机梯度下降之间,选用b个样本进行梯度下降
-
-
Mini-Batch 步骤:
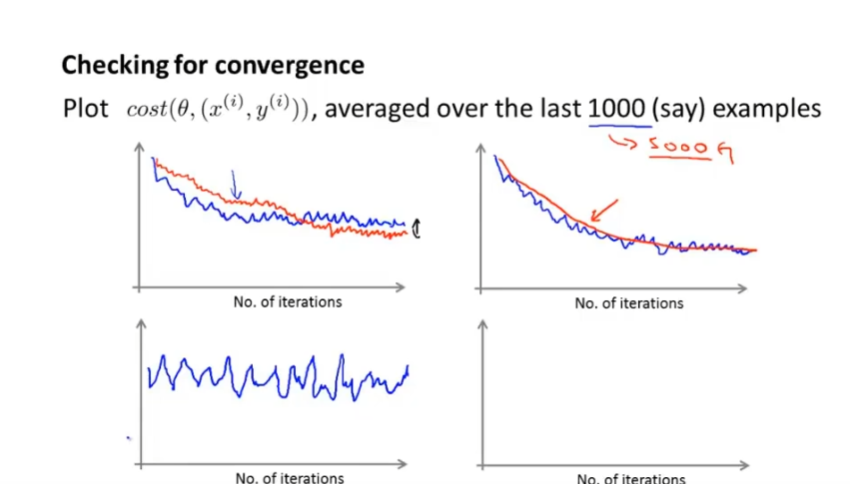
15.3 随机梯度收敛
- 思想:不是每一步进行检验损失函数是否 下降,选择一个步骤间隙,每隔一个大步骤计算损失函数平均值 并检查与前一大步 损失函数是否下降
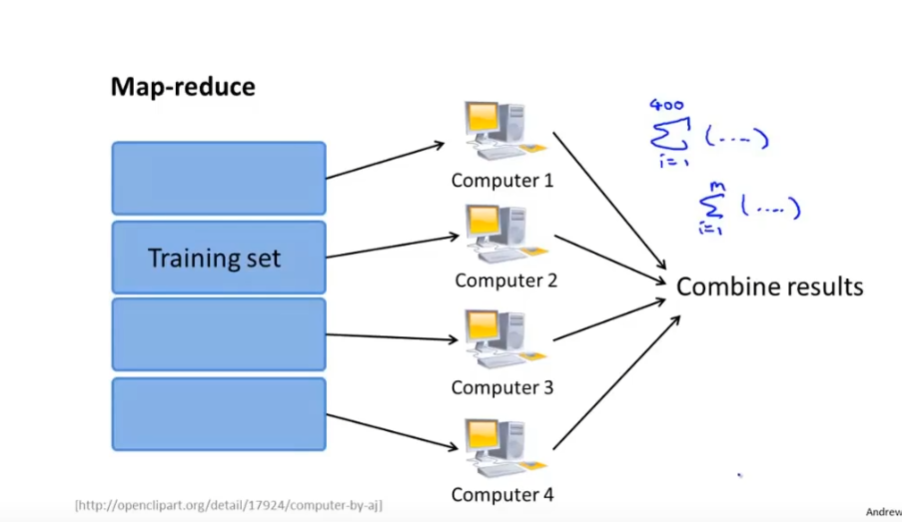
15.4 减少映射与数据并行(Map Reduce)
-
思想:
-
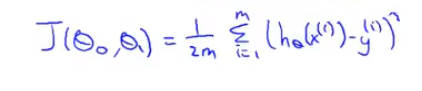











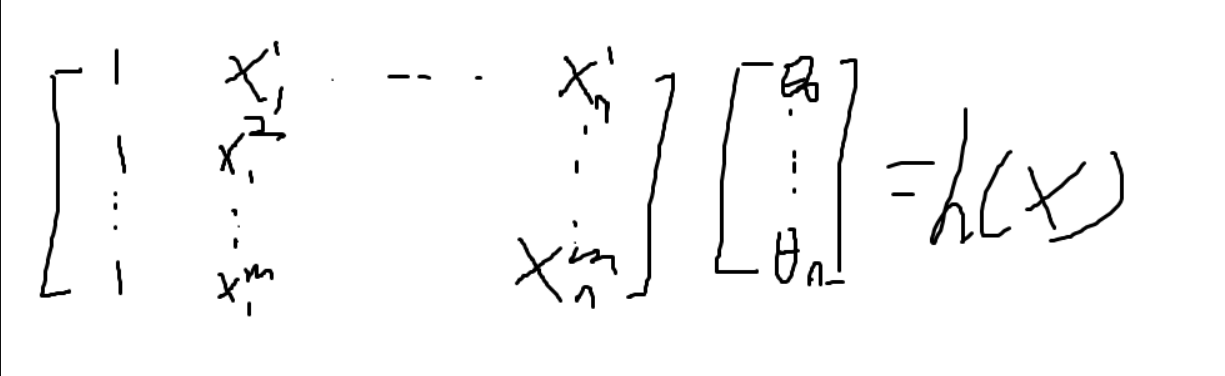
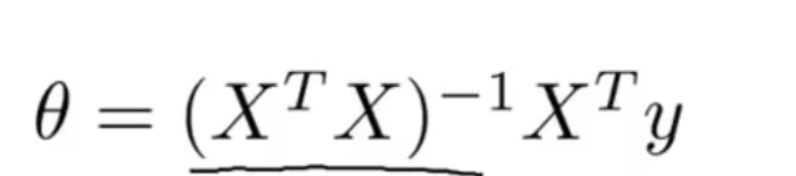











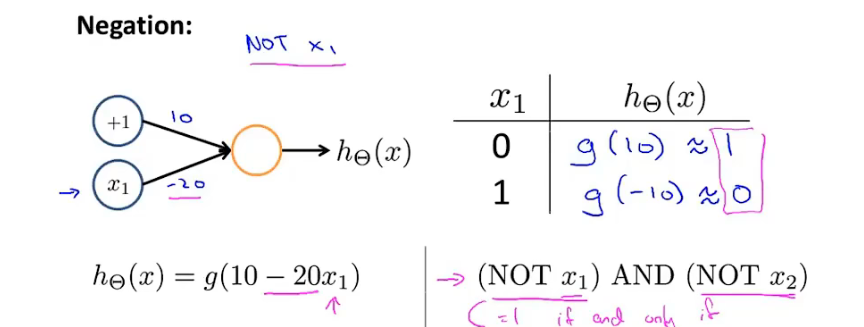
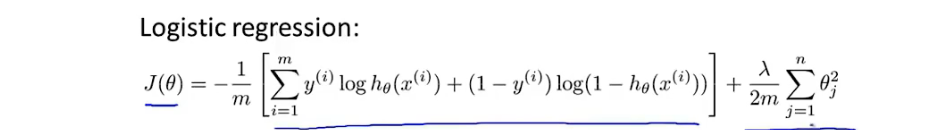



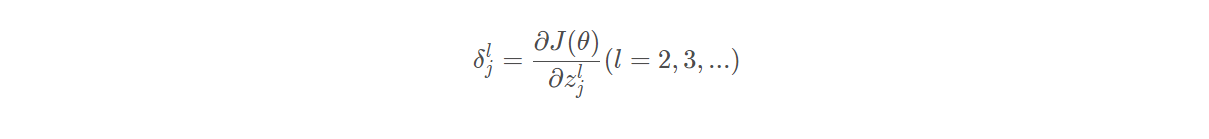
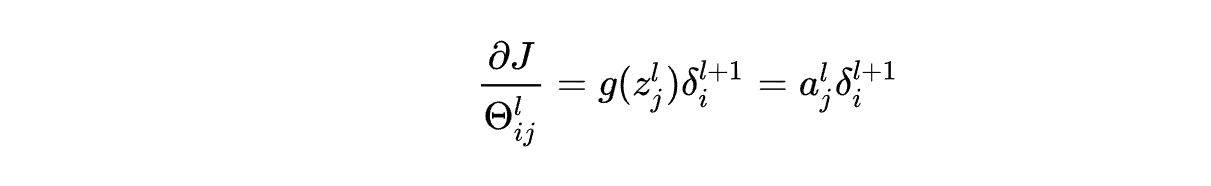
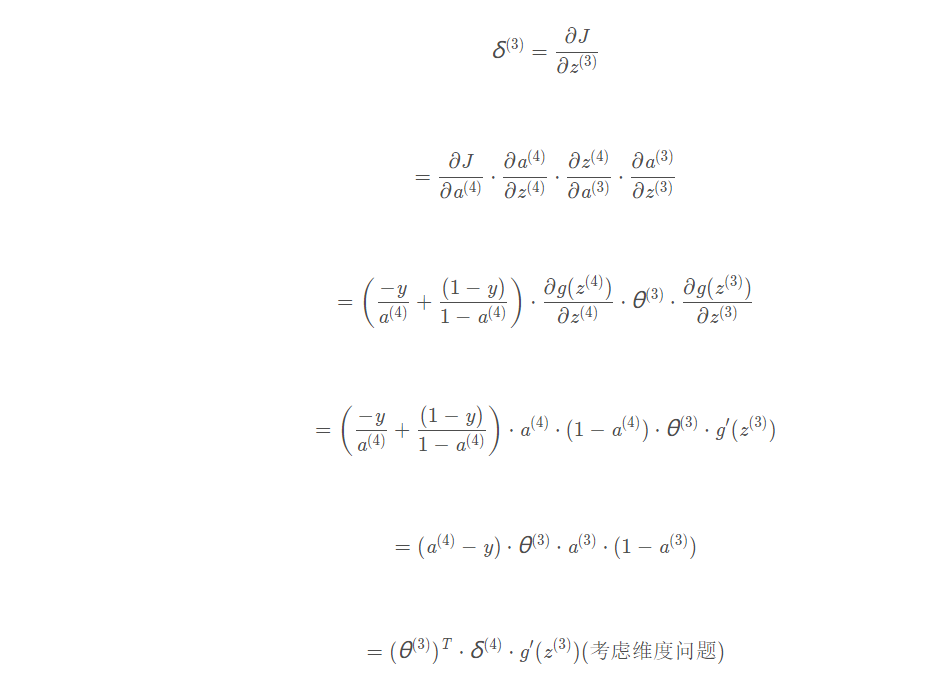


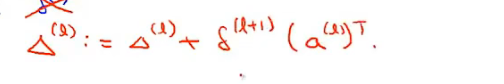

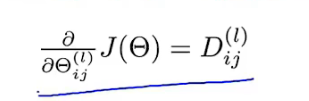
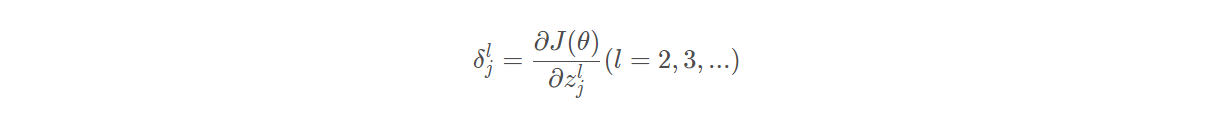
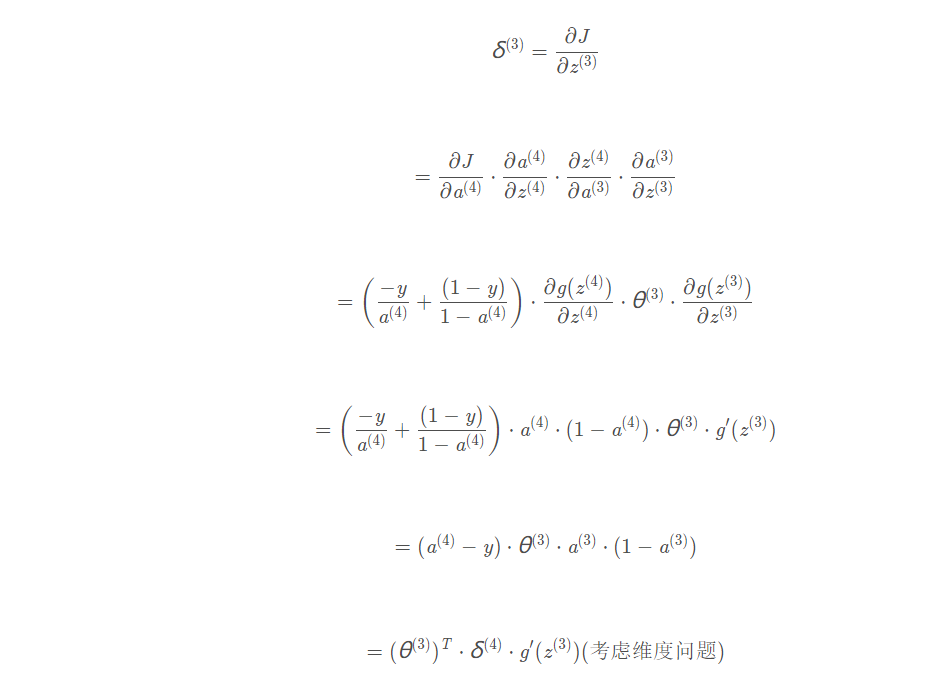
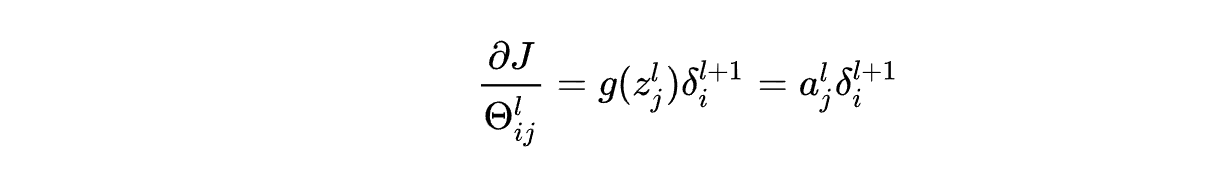









 -
-